Importance of Yield Strength & Plastic Deformation to Civil Engineers

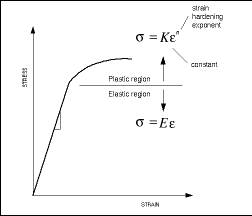
When metals are being stressed in tension at relatively low levels, the applied stress is linearly proportional to the induced strain, i.e. elastic deformation. The relationship between the applied stress, s and the strain being induced, e is as follows:

Elastic deformation is nonpermanent, i.e. the material returns to its original shape and size after the applied stress (load) is released.

When the applied stress exceeds the elastic region, plastic deformation takes place, i.e. the applied stress is no longer proportional to the strain. The point where the nonlinearity of the stress-strain relationship begins is known as the proportional limit. The applied stress is related to the induced strain in the plastic deformation region by the following equation:

where K and n are constants that differs between alloys. The parameter n is termed as the strain hardening exponent.

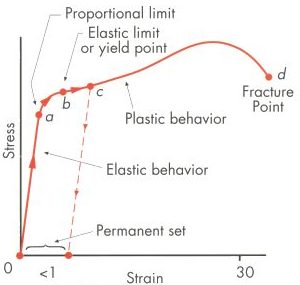
Yield stress is the stress level at the point where the material begins to have permanent deformation, i.e. yield point where the material no longer returns to its original shape and size after the release of the applied stress. However not all material will have a well defined yield region. In the absence of a distinct yield point, a 0.2% offset is used to obtain an approximate yield point. The proportional limit and the yield point are close to one another on a stress-strain curve, but they each have a different representation and thus do not corresponds to the same point on the curve.

The ultimate tensile strength is the maximum stress level on the engineering stress-strain curve, i.e. the maximum stress that can be withstand by a structure in tension. All deformation before this point is uniform throughout the narrow region of the material. After which, subsequent deformation is confined to a small constriction or neck and as the area on which the load is acting on reduces, a smaller load is required to produce a greater deformation. Ultimately, fracture occurs at the neck.

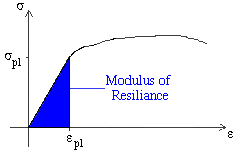
Resilience is the ability of a material to absorb energy when it is elastically deformed up to yield point and this energy is recoverable upon unloading. This value is equal to the area under the elastic region of the engineering stress-strain curve.

Toughness is the ability of a material to absorb energy up to the point of fracture. This value is equal to the entire area under the engineering stress-strain curve. When compared with the total area, resilience makes up only a small portion of the total energy that the material can absorb before failure.

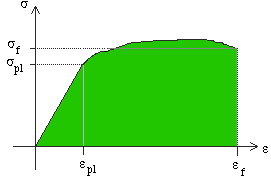
From the above definition, the value of yield strength is important in the construction of structure for civil engineers such that the structures are able to perform in the elastic region under normal servicing condition. However when faced with unexpected impact loads such as explosions, fires or natural disasters such as earthquakes, etc, the plastic region of the material becomes crucial as a large portion of the energy being absorbed by the materials under such circumstances is mainly contributed by the plastic region. As such, having a higher toughness implies that the materials are able to withstand such unforeseen loading for a longer period of time so as to allow more time for safety measures to be carried out.

In terms of failure mechanisms, there are basically two types, namely brittle fracture and ductile fracture. The table below illustrates the microscopic characteristics features of these two failure mechanisms.

	Brittle Fracture	Ductile Fracture
1.	Little or no visible plastic deformation precedes the fracture.	A large amount of plastic deformation precedes the fracture.
2.	Fracture is generally flat and perpendicular to the surface of the component.	Shear lips or dimples may be present.
3.	Fracture may appear granular or crystalline and is often highly reflective to light.	Fracture may appear to be fibrous or have a silky structure.
4.	Herring bone or chevron patterns may be present.	Necking may reduce the cross section at the fracture.
5.	Cracks lengthen very rapidly often with load noise.	Crack growth will be slow.

From the characteristics as seen above, one can easily see that ductile fracture is preferred over brittle fracture in structure constructions. This is mainly due to the fact that brittle fractures often occur suddenly without any visible warnings. As such, repair works or other appropriate safety measures can be made prior to total failure of the structure in the case of ductile failures.

A century ago, it was generalized that structures are to be designed in an elastic manner and the maximum stress is calculated according to the theory of elasticity. The allowable stress was to be much smaller than the material strength or yield limit. However it was later realized that this is a wasteful way as many structures actually redistribute stresses in such a way that the structure fails at a much higher load.

A more realistic method in the calculation of the collapse load of the structure is using the minimum expected value of material strength or yield limit, and then make sure that this collapse load would not be exceeded by the actual loads multiplied by a suitable safety factor (which is determined from experience and probabilistic considerations). As such the gap between the yield strength and the ultimate tensile strength should be as large as possible, providing a form of safety. If the ultimate tensile strength is close to the yield strength, the structure tends to fail suddenly without much warning or signs of failures and this is undesirable. This can be represented by the yield/tensile ratio, which is the ratio of the yield strength to the ultimate tensile strength.

Another contribution to steel failures is by thermal loading and the factors affecting this area are the thermal expansion coefficient and thermal conductivity of the material. Thermal loading can arise from either hot sources or from cold sources. Hot sources include hot gasses, fire, proximity to heat sources such as boilers, incinerators, etc. Cold sources include low temperature process flow, low temperature storage, low ambient temperatures such as extreme winter temperatures, etc.

Thermal expansion coefficient is defined as the proportionality constant that relates an increase in length, area or volume to its original length, area or volume as a result of an increased in temperature. For a linear thermal expansion, the following equation relates the change in length, DL, the change in temperature, DT, the initial length, L_i and the linear coefficient of thermal expansion, a:

For a volumetric thermal expansion, the change in volume, DV, change in temperature, DT, initial volume, V_i and the volume coefficient of thermal expansion, b are related as follows:

Most materials contracts upon cooling to solidification except in the case of antimony, bismuth, gallium and water which expands upon solidification. When a material is heated or cooled with its movements being restricted, possible cracking may occur due to the expansion or contraction of the material and this can cause damages the structure. As such, steel structures such as bridges are constructed with gaps for cases of thermal expansion.

The coefficient of thermal expansion is temperature dependent and its value increases with temperature. The units for the thermal expansion coefficient are (°C)^-1 or (°F)^-1.

Thermal conductivity, k is the material property that quantifies the rate of flow of thermal energy through a material in the presence of a temperature gradient. This value is stated by the amount of heat transfer across a unit area, Q/A in a unit amount of time, divided by the negative of the rate of change in temperature in the direction perpendicular to the unit area, DT/Dx. The unit is W/m.°C. The mathematical equation is:

The mechanisms of heat conduction in solid materials are by lattice vibration waves and free electrons. Thermal conductivity increases with increasing free electron concentrations since there are more free available electrons for the heat transfer process. Thermal conductivity is also temperature sensitive.

The following table shows the thermal expansion coefficient and thermal conductivity of some steels.

	Temperature	SUS410	SUS405	SUS444	SUS304	SUS316	Mild Steel
Thermal conductivity (W/m. °C)	100°C	24.9	25.1	25.9	16.3	16.3	57.7
Thermal conductivity (W/m. °C)	500°C	28.7	-	-	21.5	21.5	41.0
Thermal expansion coefficient (x10^-6/°C)	0 - 100°C	9.9	11.0	10.6	17.3	16.0	11.7
Thermal expansion coefficient (x10^-6/°C)	0 - 650°C	11.7	13.5	11.5	18.9	18.5	14.6

Temperature also has certain effects on the mechanical properties of structural steels. The elastic modulus and yield point decreases with increasing temperature. As such, the material is absorbing a lesser amount of energy within the elastic region and the structure will undergo a larger deflection with a lower stress level at higher temperatures.

Deflections developed in structures can be caused either by thermal expansion of the material or by mechanical strains. In the case of a fire, as the beams and columns of the structure are restricted to movement, thermal expansion is being restrained. This often can create beneficial mechanical strains (compression) in the structure that allow much greater bending strengths to be exploited.

However such thermal expansion can at the same time create some detrimental effects. Thermal expansion of the internal structural members or the floor system causes horizontal displacements of the exterior columns. This creates additional abnormal loadings in the columns in the lower storeys of the structure that are undesirable. As such a limit has to be placed on the outward displacement of the structure’s exterior columns.

Constant research and development in such areas is crucial as not only reduces property damages and costs but more importantly, to bring human losses and injuries to the minimum.

1. Lawrence H. Van Vlack, Elements of Material Science & Engineering, 4^th Edition, Addison Wesley, 1980, p 416-417

3. William D. Callister, Jr, Material Science and Engineering: An Introduction, 3^rd Edition, John Wiley & Sons, Inc., 1994, p 326-327